DIY QR Decoder in Python (V2: error correction)
Version 2: implementing error correction. Old one is HERE
Walkthrough to code a Python script that can read QR code, and decode it.
OpenCV actually has some built-in function to directly decode QR code (cf QRCodeDetector), that would be way more reliable than this implementation.
However, the goal here is to do a simple and crude implementation by ourself to demonstrate how it can be done with simple computer vision methods, and few lines of codes. This implementation is far from beeing perfect, nor optimized.
Limitations:
- Computer vision: Do not check nor correct the image orientation.
- Check HERE how it can be done
- Decoding: The only implementation is decoding QR Version 1 (21x21), byte-encoded
Part 1 - Image processing
The first part is dedicated at reading the QR code from an image. The goal is to end up with a binary matrix that is the representation of the QR code image
Load QR code
Load your QR code image, and import the required python modules.
import cv2
import numpy as np
from matplotlib import pyplot as plt
plt.rcParams["figure.figsize"] = (10,10)
# open your QR image
#img = cv2.imread("samples/QR.png", cv2.IMREAD_COLOR) # open in grayscale
img = cv2.imread("samples/QR_error.png", cv2.IMREAD_COLOR) # open in grayscale
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY) #convert to gray
plt.imshow(img)
<matplotlib.image.AxesImage at 0x21217135100>

The blue mark is a made-up error. This is to show later the error correction feature.
Preprocessing - Prepare the image
As a pre-processing step, we only apply a threshold on the image so that we only deal with binary pixels, either fully white, or black.
In a real world use case, where the picture might comes from a smartphone camera, we would have to perform other and more complicated preprocessing of the image. Especially to deal with scale and orientation. SIFT could be the way to deal with that. We don’t want to add this complexity here.
# thresholding, all pixel > 120 will be set to 255, the other to 0
_, gray = cv2.threshold(gray, 120, 255, cv2.THRESH_BINARY)
#plt.imshow(gray, cmap='gray')
Processing - Extract the bits
Multiple steps are needed here to achieve this goal.
3 corners
Find the QR code features (ie the 3 corners)
# find all countour
cnts, hierarchies = cv2.findContours(gray, cv2.RETR_TREE, cv2.CHAIN_APPROX_SIMPLE)
# find the 3 corners
# corners are countour with exactly 2 child
idx_of_interest = []
for i in range(len(cnts)):
cnt = cnts[i]
hierarchy = hierarchies[0][i]
child_nb = 0
while(hierarchy[2] != -1): # [Next, Previous, First_Child, Parent]
hierarchy = hierarchies[0][hierarchy[2]]
child_nb += 1
if(child_nb == 2):
idx_of_interest.append(i)
corners = np.empty((0, 4))
for i in idx_of_interest:
cnt = cnts[i]
x,y,w,h = cv2.boundingRect(cnt)
x,y,w,h = x,y,w-1,h-1
# corners should have the same width & height
if(np.abs(w-h)<3):
corners = np.append(corners, np.array([[x,y,w,h]]), axis=0)
# draw the overall region of interest = QR code area
x_min = np.min(corners, axis=0)[0]
y_min = np.min(corners, axis=0)[1]
x_max = np.max(corners, axis=0)[0] + corners[np.argmax(corners, axis=0)[0]][2] # x + w
y_max = np.max(corners, axis=0)[1] + corners[np.argmax(corners, axis=0)[1]][3] # y + h
ROI = [int(x_min), int(y_min), int(x_max), int(y_max)]
cv2.rectangle(img, (ROI[0], ROI[1]), (ROI[2], ROI[3]), (0,0,255), 1)
# draw the corner on the original img
for corner in corners:
x,y,w,h = round(corner[0]), round(corner[1]), round(corner[2]), round(corner[3])
cv2.rectangle(img, (x, y), (x + w, y + h), (255,0,0), 1)
plt.imshow(img[ROI[1]:ROI[3], ROI[0]:ROI[2]])
<matplotlib.image.AxesImage at 0x21217331c40>

Build the grid
From the 3 corners, we can estimate the cell (=bit) size, and construct the grid for reading the individual bits
# each corner should be a 7x7 cell size
# knowing that, we can estimate the cell size
cell_size = (np.mean(corners, axis=0)[2]-1) / 7
nb_cell_x = round((ROI[2] - ROI[0]) / cell_size)
nb_cell_y = round((ROI[3] - ROI[1]) / cell_size)
assert nb_cell_x == nb_cell_y
std_size = [21, 25, 29, 33, 37, 41, 45, 49, 53, 57, 61, 65, 69, 73, 77, 81, 85, 89, 93, 97, 101, 105]
# find closest standard cell number
nb_cell_x = min(std_size, key=lambda x:abs(x-nb_cell_x))
nb_cell = nb_cell_x
# affine cell_size
cell_size = (ROI[2] - ROI[0]) / nb_cell_x
print("Cell size: {} px, nb cell: {}x{}".format(cell_size, nb_cell, nb_cell))
#draw grid
for i in range(nb_cell + 1):
x = round(ROI[0] + i*cell_size)
y = round(ROI[1] + i*cell_size)
cv2.line(img, (x, ROI[1]), (x, ROI[3]), (0, 255, 0), 1) # vertical
cv2.line(img, (ROI[0], y), (ROI[2], y), (0, 255, 0), 1) # horizontal
plt.imshow(img[ROI[1]:ROI[3], ROI[0]:ROI[2]])
Cell size: 10.904761904761905 px, nb cell: 21x21
<matplotlib.image.AxesImage at 0x212174f4b20>
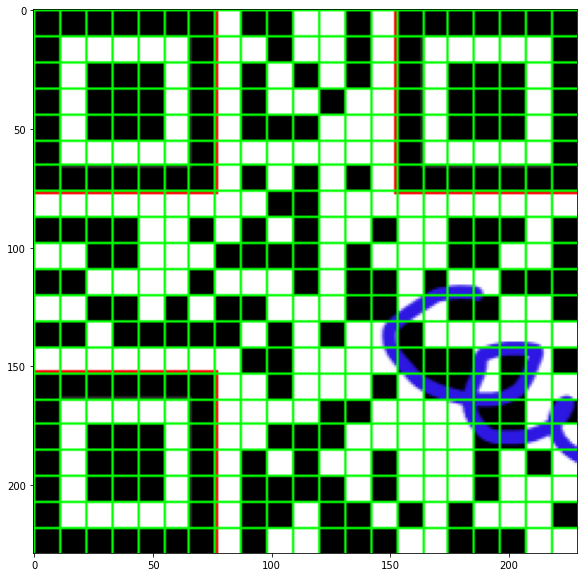
Extract the bits
Now that we have the grid, we can simply use it the extract the bit value, black or white (1 or 0). To read the bit value, we average the pixels within the cell and apply a threshold. To be more reliable, we use a gaussian kernel to average the cell pixels, so that the middle pixel in a cell has more weight than the ones on the side. This helps if the grid is not precise.
# extract bit value, from gray img
raw_bit_matrix = np.zeros((nb_cell, nb_cell), int)
for i in range(nb_cell):
for j in range(nb_cell): #X
# compute avg pixel value in the cell
x1, x2 = round(ROI[0] + i*cell_size), round(ROI[0] + (i+1)*cell_size)
y1, y2 = round(ROI[1] + j*cell_size), round(ROI[1] + (j+1)*cell_size)
# compute the average pixel val, with a Gaussian filter to give more weight to middle pixels
pixel_avg = np.mean(cv2.GaussianBlur(gray[y1:y2, x1:x2],(5,5),0))
#pixel_avg = np.mean(gray[y1:y2, x1:x2])
bit_val = 1 if pixel_avg < 140 else 0
raw_bit_matrix[j,i] = bit_val
print(raw_bit_matrix)
plt.imshow(1-raw_bit_matrix, cmap='gray') # 1-matrix to invert the color
[[1 1 1 1 1 1 1 0 1 1 0 0 1 0 1 1 1 1 1 1 1]
[1 0 0 0 0 0 1 0 0 1 0 0 1 0 1 0 0 0 0 0 1]
[1 0 1 1 1 0 1 0 1 0 1 0 1 0 1 0 1 1 1 0 1]
[1 0 1 1 1 0 1 0 1 0 0 1 0 0 1 0 1 1 1 0 1]
[1 0 1 1 1 0 1 0 1 1 1 0 0 0 1 0 1 1 1 0 1]
[1 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 1]
[1 1 1 1 1 1 1 0 1 0 1 0 1 0 1 1 1 1 1 1 1]
[0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0]
[1 1 1 1 0 0 1 0 1 0 1 0 0 1 0 0 1 1 1 0 1]
[0 0 1 1 0 0 0 1 1 1 1 0 1 0 0 0 1 1 0 0 1]
[1 1 0 0 0 0 1 0 0 0 1 0 1 1 0 1 0 0 1 1 1]
[0 0 1 1 0 1 0 1 1 0 0 0 1 1 1 0 1 1 0 0 1]
[1 1 0 1 1 1 1 1 0 1 0 1 0 0 1 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 1 1 0 0 0 0 1 1 1 1 1 1 1]
[1 1 1 1 1 1 1 0 0 1 0 0 0 1 0 1 1 0 1 0 0]
[1 0 0 0 0 0 1 0 0 0 0 1 1 0 0 0 0 1 1 0 1]
[1 0 1 1 1 0 1 0 0 1 1 1 0 0 0 0 0 1 1 1 1]
[1 0 1 1 1 0 1 0 1 0 1 0 0 1 0 0 0 1 0 1 0]
[1 0 1 1 1 0 1 0 1 1 1 1 0 1 0 0 0 1 0 0 0]
[1 0 0 0 0 0 1 0 1 1 0 1 1 0 1 0 1 0 0 0 1]
[1 1 1 1 1 1 1 0 1 0 0 1 1 1 0 0 1 1 1 0 0]]
<matplotlib.image.AxesImage at 0x212178cbf40>

Part 2 - Decoding
Limitation: Only decode Version 1 (21x21), byte-encoded QR code. Bigger QR code, and not byte-encoded are not implemented.
Encoding and Masking
The first thing to do is to read the QR format information, especially the mask number applied:
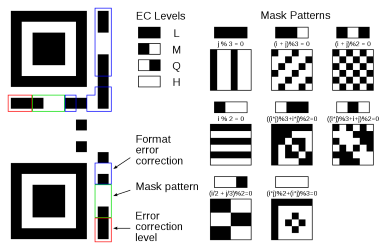
(Source: Wikipedia)
Once the mask is known, we need to apply the mask on the grid and invert the masked cell. We also check the encoding, by reading the 2x2 bottom right corner. This implementation only deals with byte encoding.
assert nb_cell == 21 # only implementation
# mask pattern
def generate_mask(mask_pattern, nb_cell):
""" Generate the mask to apply on the matrix """
def add_fixed_mask(mask, nb_cell):
""" generate the fixed mask used on the format bits """
fm = np.zeros((nb_cell, nb_cell), int)
for i in [0, 2, 4, 16, 19]:
fm[8,i] = 1
fm[nb_cell-i-1,8] = 1
return np.add(mask, fm)
def remove_fixed_pattern_from_mask(mask, nb_cell):
""" The mask is only applied to the data, not the fixed pattern """
fm = np.ones((nb_cell, nb_cell), int)
fm[0:9, 0:9] = 0 # remove top-left feature and format
fm[nb_cell-8:nb_cell, 0:9] = 0 # remove bottom-left feature and format
fm[0:9, nb_cell-8:nb_cell] = 0 # remove top-right feature and format
fm[6, :] = 0
fm[:, 6] = 0
return np.multiply(mask, fm)
def generate_main_mask(mask_pattern):
""" generate the main mask """
if(np.array_equal(mask_pattern, np.array([0, 0, 0]))):
def mask_gen(i, j):
bit = 1 if((i+j)%2 == 0) else 0
return bit
elif(np.array_equal(mask_pattern, np.array([0, 0, 1]))):
def mask_gen(i, j):
bit = 1 if(i%2 == 0) else 0
return bit
elif(np.array_equal(mask_pattern, np.array([0, 1, 0]))):
def mask_gen(i, j):
bit = 1 if(j%3 == 0) else 0
return bit
elif(np.array_equal(mask_pattern, np.array([0, 1, 1]))):
def mask_gen(i, j):
bit = 1 if((i+j)%3 == 0) else 0
return bit
elif(np.array_equal(mask_pattern, np.array([1, 0, 0]))):
def mask_gen(i, j):
bit = 1 if((i/2+j/3)%2 == 0) else 0
return bit
elif(np.array_equal(mask_pattern, np.array([1, 0, 1]))):
def mask_gen(i, j):
bit = 1 if( (i*j)%2 + (i*j)%3 == 0) else 0
return bit
elif(np.array_equal(mask_pattern, np.array([1, 1, 0]))):
def mask_gen(i, j):
bit = 1 if( ((i*j)%3 + (i*j))%2 == 0) else 0
return bit
elif(np.array_equal(mask_pattern, np.array([1, 1, 1]))):
def mask_gen(i, j):
bit = 1 if( ((i*j)%3 + i + j)%2 == 0) else 0
return bit
mask = np.zeros((nb_cell, nb_cell), int)
for i in range(nb_cell):
for j in range(nb_cell):
mask[i, j] = mask_gen(i,j)
return mask
# generate the main mask
mask = generate_main_mask(mask_pattern)
# remove fixed pattern from the mask
mask = remove_fixed_pattern_from_mask(mask, nb_cell)
# add the fixed mask on the format region
final = add_fixed_mask(mask, nb_cell)
return final
# find the correct mask and generate it
mask_pat_hor = np.flip(raw_bit_matrix[8, 2:5])
mask_pat_ver = np.flip(raw_bit_matrix[nb_cell-5:nb_cell-2, 8])
assert mask_pat_hor[0] == mask_pat_ver[2] and mask_pat_hor[2] == mask_pat_ver[0] and mask_pat_hor[1] == mask_pat_ver[1]
print("Mask pattern: {}".format(mask_pat_hor))
mask = generate_mask(mask_pat_hor, nb_cell)
plt.imshow(1-mask, cmap='gray') # 1-matrix to invert the color
Mask pattern: [0 1 1]
<matplotlib.image.AxesImage at 0x21217a51130>

Here is the mask.
Now we need to apply this mask on our matrix of bits, and read some information as encoding and error correctino level.
def get_encoding(unmasked_matrix, nb_cell):
""" retreive the encoding of the QR Code """
enc = unmasked_matrix[nb_cell-2:nb_cell, nb_cell-2:nb_cell]
# ensure it is byte encoded (only implementation supported)
assert np.array_equal(enc, np.array([[0, 0], [1, 0]]))
return enc
def get_err_lvl(unmasked_matrix, nb_cell):
""" retreive the error correction level in use """
ec_level_hor = unmasked_matrix[8, 0:2]
ec_level_ver = unmasked_matrix[nb_cell-2:nb_cell, 8]
assert ec_level_hor[0] == ec_level_ver[1] and ec_level_hor[1] == ec_level_ver[0]
ec_level_txt = ''
ec_nb_bytes = 0
if(np.array_equal(ec_level_hor, np.array([0, 1]))):
ec_level_txt, ec_nb_bytes = '7%', 7
elif(np.array_equal(ec_level_hor, np.array([0, 0]))):
ec_level_txt, ec_nb_bytes = '15%', 10
elif(np.array_equal(ec_level_hor, np.array([1, 1]))):
ec_level_txt, ec_nb_bytes = '25%', 13
elif(np.array_equal(ec_level_hor, np.array([1, 0]))):
ec_level_txt, ec_nb_bytes = '30%', 17
return (ec_level_txt, ec_nb_bytes)
# apply mask on matrix
unmasked_matrix = np.bitwise_xor(raw_bit_matrix, mask)
plt.imshow(1-unmasked_matrix, cmap='gray') # 1-matrix to invert the color
# check encoding, make sure it is byte-encoded (only implementation)
enc = get_encoding(unmasked_matrix, nb_cell)
print("Encoding pattern: \n{}".format(enc))
# Error correction level
ec_level_txt, ec_nb_bytes = get_err_lvl(unmasked_matrix, nb_cell)
print("Error corr level: {}".format(ec_level_txt))
Encoding pattern:
[[0 0]
[1 0]]
Error corr level: 7%

Read the data
Finally, we can read the data, block by block, following this format. Note that the number of data blocks VS the number of error blocks depends on the error correction level.
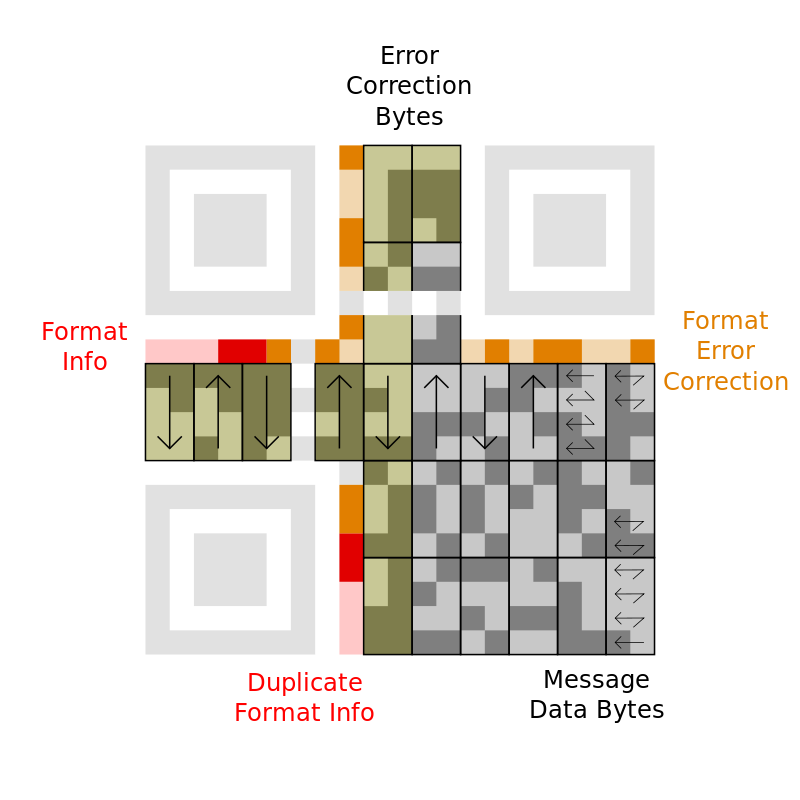
(Source: Wikipedia)
def bit_list_to_bytes_list(bit_list):
mapped = "".join(map(str, bit_list))
return [int(mapped[i:i+8], 2) for i in range(0, len(mapped), 8)]
def read_21x21_bits(qr_matrix):
def build_reading_order_bit_idx():
# read 15 first block pattern (=15x8 = 120 bits)
bit_idx = [] # x,y
# add indices of 15 first block pattern (3x5 block pattern with alterning read direction)
down_up = True
for y in range(20,10,-2):
rng = []
if(down_up):
rng = range(20,8,-1) # down-up reading direction
else:
rng = range(9,21,1) # up-down reading direction
for x in rng:
bit_idx.append((x,y))
bit_idx.append((x,y-1))
down_up = not down_up # inverse direction
# read next block (down up)
y = 12
for x in [8, 7, 5, 4, 3, 2, 1, 0]:
bit_idx.append((x,y))
bit_idx.append((x,y-1))
# read next (up down)
y = 10
for x in [0, 1, 2, 3, 4, 5, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20]:
bit_idx.append((x,y))
bit_idx.append((x,y-1))
# read next (alternating)
down_up = True
for y in [8, 5, 3, 1]:
rng = []
if(down_up):
rng = [12, 11, 10, 9] # down-up reading direction
else:
rng = [9, 10, 11, 12] # up-down reading direction
for x in rng:
bit_idx.append((x,y))
bit_idx.append((x,y-1))
down_up = not down_up # inverse direction
return bit_idx
bit_idx = build_reading_order_bit_idx()
data_bit_list = []
for (x, y) in bit_idx:
data_bit_list.append(qr_matrix[x, y])
return data_bit_list
# read all raw bits in the correct order
all_bits = read_21x21_bits(unmasked_matrix)
all_bytes = bit_list_to_bytes_list(all_bits)
# shit by 4 to skip the small 2x2 bloc with encoding information
# and read the rest of the data by block of 8
all_bytes_shifted = bit_list_to_bytes_list(all_bits[4:])
# the first bloc is the message length, then it is the data
msg_length_bloc = all_bytes_shifted[0]
data_decoded = ""
for b in all_bytes_shifted[1:msg_length_bloc+1]:
data_decoded += chr(b)
print('msg length: {}'.format(msg_length_bloc))
print('msg: {}'.format(data_decoded))
msg length: 6
msg: Sojgra
The above decoded data doesn’t make a lot of sense. This is due to the error we intentionally added in the original QR Code (the blue mark)
Luckily, QR code have some error correction features. Let’s try
Error correction
QR code implements error correction. The algorithm in use is called Reed Solomon. It is widely used and is quite powerful. unfortunately, the theory behind is quite complex. We won’t deal with how it works here. We are only showing how to use it in our case thanks to the python library called reedsolo
We will apply the error correction on the data only. Normally we should also check about errors in the fixed format info
from reedsolo import RSCodec
# determine the number of data bytes VS the numner of error bytes
data_lvl_bytes = 26-ec_nb_bytes
data_bytes = all_bytes[0:data_lvl_bytes]
err_bytes = all_bytes[data_lvl_bytes:]
# perform the Reed Solomon decoding
rsc = RSCodec(ec_nb_bytes)
decoded_msg, decoded_msgecc, errata_pos = rsc.decode(all_bytes)
if(len(list(errata_pos)) > 0):
for e in list(errata_pos):
print('error in bloc: ', e)
else:
print('No error')
error in bloc: 9
error in bloc: 4
error in bloc: 1
def bytes_to_bit_list(byts):
bit_list = []
for b in byts:
for i in range(8):
if((b>>(7-i)) & 1):
bit_list.append(1)
else:
bit_list.append(0)
return bit_list
# show the final decoded message
bits = bytes_to_bit_list(decoded_msg)
# shift by 4 bits (same reason as before, skip encoding 2x2 bloc)
shifted_decoded_bytes = bit_list_to_bytes_list(bits[4:])
msg_length_bloc = shifted_decoded_bytes[0]
data_decoded = ""
for b in shifted_decoded_bytes[1:msg_length_bloc+1]:
data_decoded += chr(b)
print('msg length: {}'.format(msg_length_bloc))
print('msg final: {}'.format(data_decoded))
msg length: 10
msg final: Congrats !
That’s it ! We manage to decode “manually” this QR code. As said before, this code is just a demonstration on how it can be done with simple steps using python. It is not reliable and the implementation is not complete.
Interesting things to try:
- Pre-processing: deal with distorded images, align features
- Decoding: Deal with more encoding
- Perform error correction on fixed info pattern